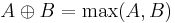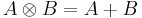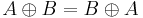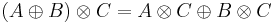Max-plus algebra

A max-plus algebra is an algebra over the real numbers with maximum and addition as the two binary operations. It can be used appropriately to determine marking times within a given Petri net and a vector filled with marking state at the beginning.

1 Operators
- 1.1 Scalar operations
- 1.2 Matrix operations
2 Useful enhancement elements
3 Algebra properties
4 See also
5 Additional reading
6 External links

Operators

Scalar operations

Let A and B be scalars. Then the operations maximum (implied by the max operator $\oplus$ ) and addition (plus operator $\otimes$ ) for this scalars are defined as

$A \oplus B = \max(A,B)$

$A \otimes B = A %2B B$

Watch: Max-operator $\oplus$ can easily be confused with the addition operation. All $\otimes$ - operations have a higher precedence than $\oplus$ - operations.

Matrix operations

Max-Plus algebra can be used for matrix operands M, N likewise. To perform the 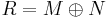$R = M \oplus N$ - operation, the elements of the resulting matrix R (row i, column j) have to be set up by the maximum operation of both corresponding elements of the matrices M and N:

R_ij = M_ij $\oplus$ N_ij

The $\otimes$ - operation is similar to algorithm of Matrix multiplication, however, every "+" calculation has to be substituted by a $\oplus$ - operation, every " $\cdot$ " calculation by a $\otimes$ - operation.

Useful enhancement elements

In order to handle marking times like 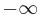$-\infty$ which means "never before", the ε-element has been established by ε 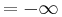$=-\infty$ . According to the idea of infinity, the following equations can be found:

ε $\oplus$ A = A

ε $\otimes$ A = ε

To point the zero number out, the element e was defined by 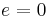$e=0$ . Therefore:

e $\otimes$ A = A

Obviously, ε is the neutral element for the $\oplus$ - operation as well as e is for the $\otimes$ - operation

Algebra properties

associativity:

$(A \oplus B) \oplus C = A \oplus (B \oplus C)$

$(A\otimes B) \otimes C = A \otimes (B \otimes C)$

commutativity :

$A \oplus B = B \oplus A$

distributivity:

$(A \oplus B) \otimes C = A \otimes C \oplus B \otimes C$

Note: In general, A $\otimes$ B = B $\otimes$ A does not hold, for example in the case of matrix operations.

Additional reading

Butkovič, Peter (2010), Max-linear Systems: Theory and Algorithms, Springer Monographs in Mathematics, Springer-Verlag, doi:10.1007/978-1-84996-299-5